Эксцентрисите́т — числовая характеристика конического сечения, показывающая степень его отклонения от окружности. Обычно обозначается ${\displaystyle e}$ или ${\displaystyle \varepsilon }$.

Эксцентриситет инвариантен относительно движений плоскости и преобразований подобия.

Определение

Все невырожденные конические сечения, кроме окружности, можно описать следующим способом: выберем на плоскости точку ${\displaystyle F}$ и прямую ${\displaystyle d}$ и зададим вещественное число ${\displaystyle e>0}$; тогда геометрическое место точек ${\displaystyle M}$, для которых отношение расстояний до точки ${\displaystyle F}$ и до прямой ${\displaystyle d}$ равно ${\displaystyle e}$, является коническим сечением; то есть, если ${\displaystyle M'}$ есть проекция ${\displaystyle M}$ на ${\displaystyle d}$, то

${\displaystyle FM=e\cdot MM'}$.

Это число ${\displaystyle e}$ называется эксцентриситетом конического сечения. Эксцентриситет окружности по определению равен 0.

Связанные определения

• Точка ${\displaystyle F}$ называется фокусом конического сечения.
• Прямая ${\displaystyle d}$ называется директрисой.

Коническое сечение в полярных координатах

Коническое сечение, один из фокусов которого находится в полюсе, задаётся в полярных координатах уравнением:

${\displaystyle r={\frac {\ell }{1-e\cos \varphi }}}$,

где ${\displaystyle e}$ — эксцентриситет, а ${\displaystyle \ell }$ — другой постоянный параметр (так называемый фокальный параметр).

Легко показать, что это уравнение эквивалентно определению, данному выше. В сущности, оно может быть использовано в качестве альтернативного определения эксцентриситета, быть может, менее фундаментального, но удобного с аналитической и прикладной точек зрения; в частности, из него хорошо видна роль эксцентриситета в классификации конических сечений и определённым образом дополнительно проясняется его геометрический смысл.

Свойства

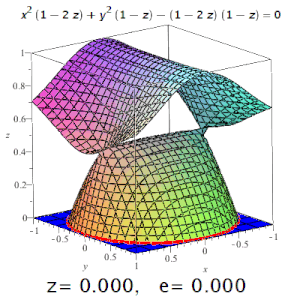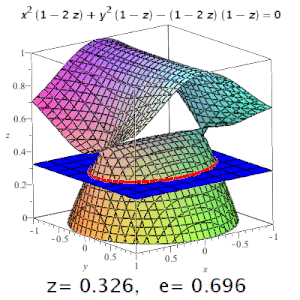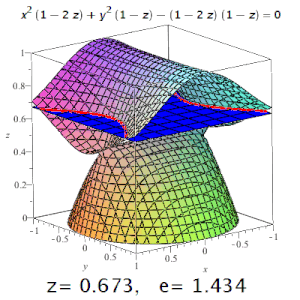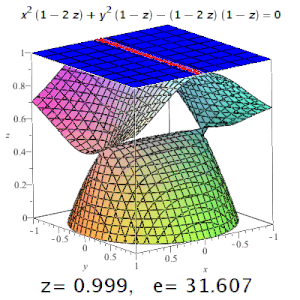
• В зависимости от эксцентриситета, получится:
  • при ${\displaystyle e>1}$ — гипербола. Чем больше эксцентриситет гиперболы, тем больше две её ветви похожи на параллельные прямые линии;
  • при ${\displaystyle e=1}$ — парабола;
  • при ${\displaystyle 0\leq e<1}$ — эллипс;
  • для окружности полагают ${\displaystyle e=0}$.

• Эксцентриситет эллипса и гиперболы равен отношению расстояния от фокуса до центра к большой полуоси. Это свойство иногда принимают за определение эксцентриситета. В прежние времена (например, в 1787 году[1]) на большую полуось не делили — эксцентриситетом эллипса называли расстояние от фокуса до центра[2].
• Эксцентриситет эллипса может быть также выражен через отношение малой (${\displaystyle b}$) и большой (${\displaystyle a}$) полуосей:

${\displaystyle e={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}}$.

• Эксцентриситет гиперболы может быть выражен через отношение мнимой (${\displaystyle b}$) и действительной (${\displaystyle a}$) полуосей:

${\displaystyle e={\sqrt {1+{\frac {b^{2}}{a^{2}}}}}}$.

• Эксцентриситет равносторонней гиперболы, являющейся графиком обратной пропорциональности и задаваемой уравнением ${\displaystyle f(x)={k \over x},x\neq 0,k\neq 0}$, равен ${\displaystyle {\sqrt {2}}}$.

• Для эллипса также может быть выражен через отношение радиусов пери- (${\displaystyle r_{\mathrm {per} }}$) и апоцентров (${\displaystyle r_{\mathrm {ap} }}$):

${\displaystyle e={\frac {r_{\mathrm {ap} }-r_{\mathrm {per} }}{r_{\mathrm {ap} }+r_{\mathrm {per} }}}=1-{\frac {2}{{\frac {r_{\mathrm {ap} }}{r_{\mathrm {per} }}}+1}}}$.

См. также

• Эксцентриситет орбиты
• Коническая константа

Примечания

Литература

• Акопян А. В., Заславский А. А. Геометрические свойства кривых второго порядка. — М.: МЦНМО, 2007. — 136 с.

На других языках

[es] Excentricidad (matemática)