astro.wikisort.org - Наука

Орбита́льные элеме́нты, элеме́нты орби́ты небесного тела — набор параметров, задающих размеры и форму орбиты (траектории) небесного тела, расположение орбиты в пространстве и место расположения небесного тела на орбите.

Определение орбит небесных тел является одной из задач небесной механики. Для задания орбиты спутника планеты, астероида или Земли используют так называемые «орбитальные элементы». Орбитальные элементы отвечают за задание базовой системы координат (точки отсчёта, о́си координат), формы и размера орбиты, её ориентации в пространстве и момент времени, в который небесное тело находится в определённой точке орбиты. В основном используются два способа задания орбиты (при наличии системы координат)[1]:

• при помощи векторов положения и скорости;
• при помощи орбитальных элементов.

Кеплеровы элементы орбиты

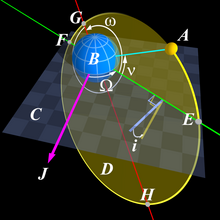
Традиционно в качестве элементов орбиты используют шесть величин, получивших название кеплеровых[2]:

• большая полуось (a);
• эксцентриситет орбиты (e);
• наклонение (i);
• аргумент перицентра (ω);
• долгота восходящего узла (☊);
• средняя аномалия (M_o).

Другие элементы орбиты

Аномалии

Анома́лия (в небесной механике) — угол, используемый для описания движения тела по эллиптической орбите. Термин «аномалия» впервые введён Аделардом Батским при переводе на латынь астрономических таблиц Аль-Хорезми «Зидж» для передачи арабского термина «аль-хеза» («особенность»).

И́стинная анома́лия (на рисунке обозначена ${\displaystyle \nu }$, так же обозначается T, ${\displaystyle \theta }$ или f) представляет собой угол между радиус-вектором r тела и направлением на перицентр.

Сре́дняя анома́лия (обычно обозначаемая M) для тела, движущегося по невозмущённой орбите, — произведение его среднего движения (средней угловой скорости за один оборот) и интервала времени после прохождения перицентра. Иными словами, средняя аномалия — угловое расстояние от перицентра до воображаемого тела, движущегося с постоянной угловой скоростью, равной среднему движению реального тела, и проходящего через перицентр одновременно с реальным телом.

Эксцентри́ческая анома́лия (обозначаемая E) — параметр, используемый для выражения переменной длины радиус-вектора r.

Зависимость r от E и ${\displaystyle \nu }$ выражается уравнениями

${\displaystyle r=a(1-e\cdot \cos E),}$

${\displaystyle r={\frac {a(1-e^{2})}{1+e\cdot \cos \nu }}}$,

где:

• a — большая полуось эллиптической орбиты;
• e — эксцентриситет эллиптической орбиты.

Средняя аномалия и эксцентрическая аномалия связаны между собой через уравнение Кеплера.

Аргумент широты

Аргуме́нт широты́ (обозначаемый u) — угловой параметр, который определяет положение тела, движущегося вдоль кеплеровой орбиты. Это сумма часто используемых истинной аномалии (см. выше) и аргумента перицентра, образующая угол между радиус-вектором тела и линией узлов. Отсчитывается от восходящего узла по направлению движения[3].

${\displaystyle u=\nu +\omega ,}$

где:

• u — аргумент широты;
• ${\displaystyle \nu }$ — истинная аномалия;
• ${\displaystyle \omega }$ — аргумент перицентра.

Аномалистический период обращения

Аномалисти́ческий пери́од обраще́ния — промежуток времени, за который тело, перемещаясь по эллиптической орбите, дважды последовательно проходит через перицентр.

Примечания

Ссылки

• Аномалия астрономическая // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.

Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист.

На других языках

---

[de] Bahnelement

Als Bahnelemente werden die Parameter bezeichnet, die die Bahn und die Bewegung eines astronomischen Objekts beschreiben, das den Keplerschen Gesetzen im Schwerefeld eines Himmelskörpers gehorcht (Zweikörperproblem).

---

[es] Elementos orbitales

Los elementos orbitales son los parámetros necesarios para identificar de forma única la órbita específica de un cuerpo celeste. En mecánica celeste estos elementos se consideran en sistemas de dos cuerpos utilizando una órbita de Kepler. Hay muchas formas diferentes de describir matemáticamente la misma órbita, pero ciertos esquemas, cada uno de los cuales consta de un conjunto de seis parámetros, se usan comúnmente en astronomía y mecánica orbital.

---

- [ru] Элементы орбиты

---

---